【CS50x(2022)】Complexity and Big O Notation

在上 CS50x 第三週的演算法時，總覺得對「時間複雜度」的理解不夠清楚，因此另外找了課程做補充。

課程連結： 資料結構與演算法(JavaScript)

演算法

什麼是演算法？

Algorithms means step-by-step instructions for solving problems. —— CS50x

簡單來說，就是解決一個特定問題的步驟的集合。這個「問題」並不是狹義上的問題，而是一個想要達成的「目標」，而演算法就是達成這個目標所需經歷的過程。

以第一週的二分搜尋法舉例，從拿到電話簿到找到電話號碼中間經過的13個步驟，就是所謂的演算法。

Input	Algorithm	Output
A phone book		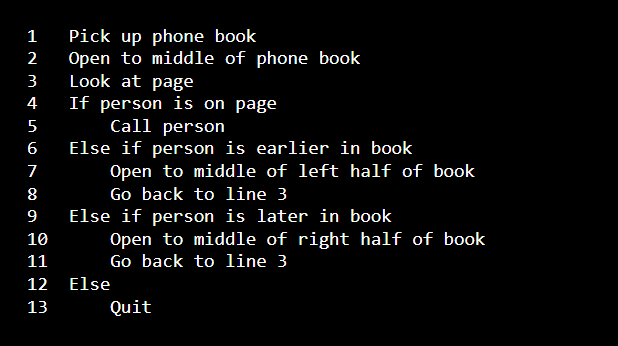Find phone number

如何比較演算法？

Time and Space are the concerns. The less time it takes, the better it is.
—— 資料結構與演算法(JavaScript)課程

解決同一個問題可以有很多種不同的方法，每個方法的效率也不一樣。一個好的演算法，就是能用更有效率的方式解決問題。在電腦科學的世界裡，通常會用兩個面向來衡量演算法的效率：

1. 時間複雜度(Time Complexity)： 如果直接為執行過程計時，通常結果會受到多方因素的影響(硬體設備、輸入資料規模…等)，所以直接計時是比較沒有參考價值的。而時間複雜度指的是執行過程中所需經過的「步驟數量」，這個在稍後會有比較詳細的說明。

2. 空間複雜度(Space Complexity)： 是指一支程式在執行時需要耗費多少的記憶體資源。

有時候我們需要在這兩者之間做取捨。就像我們平常在買電腦時一樣，如果希望電腦跑得快一點，就要多投資在硬體資源上；反之，如果想要節省硬體資源成本，可能就會花較多的時間成本。

時間複雜度

時間複雜度的計算

前面提到，時間複雜度指的是執行過程中所需經過的「步驟數量」。一個加法、減法、乘法、除法、比較…等都分別算一個步驟，不同規模的輸入資料可能會影響執行步驟的數量。例如：

1 + 2 + 3            --> 經過2個步驟
1 + 2 + 3 + 4 + 5    --> 經過4個步驟

範例一：等差級數的相加，如果使用 for 迴圈執行。則 step == n。

int addition(int n) {
  int step = 0;
  int result = 0;

  for (int i = 1; i <= n; i++) {
    result += i;
    step ++;
  }
}

範例二：等差級數的相加，如果使用梯形的面積公式執行，則 step == 3。

int addition(int n) {
  int result = (1 + n) * n / 2;  
}

範例三：雙重迴圈執行步驟，則 step == n 平方。

int addition(int n) {  
  int step = 0;

  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      step++
    }
  }
}

從上面的例子可以看出，時間複雜度常常跟 input 資料的規模 n 有一定的關聯性。通常 n 越大，需要執行的步驟也越多。

時間複雜度的表示方式

一個演算法的時間複雜度有三種：

1. Big O notation： 指「最壞」情況下需要經過的步驟數量。
2. Big Ω notation： 指「最好」情況下需要經過的步驟數量。
3. Big Θ notation： 表示「最好」和「最壞」相等的情況。

三種複雜度中，最需要考量的是 Big O notation ，因為它是衡量一個演算法「最大成本」的基準。常見的時間複雜度如下表：O(1)、O(log n)、O(n)、O(nlog n)、O(n^2)。其中， n 指的是資料規模，() 中則表示步驟數量。

在表示步驟數量時有幾個慣例：

1. Constant doesn’t matter (例如：如果執行步驟為 O(3n) 會直接用 O(n) 表示。)
2. Small Terms don’t matter (例如：如果執行步驟為 O(n^2+3n+1) 會直接用 O(n^2) 表示。)
3. Logarithm Base doesn’t matter (例如：如果執行步驟為 O(log2 n) 會直接用 O(log n) 表示。)

其原因為，如果資料量大到一定程度，以上 3 個條件對步驟數量的影響會大幅度縮小。用以下表格例子，在 n 和 n + 1500 的結果看來，當資料規模逐漸變大，除了影響最大的 n 以外，1500 的影響力在逐漸縮小。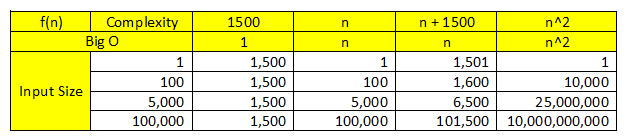

演算法的優化

由前面的說明可以看出，一個演算法的設計對執行效率有很大的影響。

拿前面的等差數列相加為例：如果使用 for 迴圈執行，則 step == n；如果使用梯形的面積公式執行，則 step == 3。

Algorithm	Step	Big O notation
for 迴圈	n	O(n)
梯形公式	3	O(1)

隨著資料量的變大， for 迴圈需要花費的時間越來越長，而梯形公式則可以維持同樣的計算時間。因此我們可以說，在計算等差數列相加時，梯形公式是一個較好的演算法。

當我們想優化演算法時，就要盡可能地將 Big O notation 降低，以達到更好的效率。

文章內容如有錯誤，歡迎留言討論！